1.1 Hexadecimal
As you might know all current computers are binary machines, which is to say they operate on the idea of a reasonably continuous feed of of 1 and 0 values to various pins to do what needs to be done. 1 and 0 get very hard to read so these are stacked up 4 deep to form hexadecimal (a very similar logic to writing things like 1x10^9 instead of 1000000000). 4 things each with the ability to be one of two different states means 16 combinations, and as it is then desirable to be able to display each combination as a single character the letters A through F join the Arabic numbers (0 through 9) to make 16 (A=10 decimal, B=11 and so on to F=15 at which time it wraps around and 10=16 decimal).
A quick reference table
| Decimal | Hexadecimal | Binary |
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
The thing to remember about binary is that it is much like the number 1567 decimal means 1 count of 1000, 5 counts of 100, 6 counts of 10 and 7 counts of 1 or in words it is a list of counts of ten raised to a power. For binary rather than ten you use 2 so 1110 means one count of 8, one count of 4, one count of 2 and zero counts of 1. There are all sorts of tricks and things you can learn here, many of which will be covered before long, and some are almost as essential as hexadecimal when it comes to understanding the document to come.
You can learn to convert it and do maths with it in your head if you like and it is certainly a useful skill, however most of the time you will just be finding the value (in which case a program will probably be doing it) and everything from windows bundled calculator (in scientific mode) upwards will convert between the various bases (base10= decimal, base2= binary, base16=hexadecimal) and be able to perform maths with it.
There is a fourth method called Octal aka base 8 that uses 0 through 7 and represents 3 bits but 3 is a terrible number to work with and multiply with (it being a prime number and all) so it tends not to be used outside of specific applications. There are further variations on this theme in things like Base64 but that is an encoding scheme for transmission of data and will be covered later in text hacking.
In summary hex(adecimal) is just a numbering scheme that works better than regular decimal for computing purposes and nothing more. Quite often new hackers are seen to assign a near magical status to hexadecimal, and by extension hex editors, when it really deserves nothing of the sort; the magical stuff is assembly hacking. Certainly it is very hard to take a look at an entire ROM and edit it just from a hex editor which is why nobody does it from scratch, if they appear to then it is almost certain they either did a lot of work to get to that point (there are many programs that will spit out locations and interesting values). Putting in the time to reverse engineer the original work is what ultimately allowed for the simple edit, failing that the file conforms to a known standard (open up any proper DS ROM and the first line will be a ASCII encoded text string of the internal name of the ROM and there are similar things for most DS files/formats) or enough of a standard that a basic edit is possible.
1.1.1 Representation
There is a very overdone computing joke along the lines of there are 10 kinds of people in the world (those that know binary and those that do not).
As said “joke” just illustrated it is hard or even impossible to know what set of numbers is being used. As you can take down an entire system with an errant bit, let alone a complete misinterpretation, there needs to be a way to indicate what is being used. In mathematics a subscript decimal value of the base you are using is used but that is awkward to write in a basic text editor so various notations have been used. The most common ones being 0x???????? (sometimes the 0x is repeated after so many values but not always), ????????h/h????????, #???????? (this is the way HTML does it but not so many ROM hackers will use it), %???????? (this is the way your browser probably signifies it with %20 for example being the ASCII text encoding for a space) or simply ???????? hex. Most people are quite happy to accept a bit of redundancy in exchange for a lack of confusion here.
Stick two hexadecimal numbers together (sometimes called nibbles/nybbles) and you have a byte. From there it can stack further although it can get a bit tricky as it varies between computer architectures (32 vs 64 bit for instance), operating systems and sometimes programming languages. In general most people will stick to the 32 bit C programming language interpretations of all this and that is what this document will be using unless otherwise stated.
Going further the terms halfword, word, double word (dword), quad word, short, long and int are what is interesting and are probably worth knowing.
Most of the time it follows on from bytes with half word being 16 bits aka 2 bytes, words being 32 bits aka 4 bytes, dwords being 64 bits and so on. In ROM hacking few people will use the terms short and long and especially not the term “int” as the “bit” of the processor in question will vary this, the main exception being if they are defining a format in a similar manner used in a programming language (in which case uint for unsigned integer, u8, u16 and similar things appear). If you do go looking “typedef” is the usual catch all term to describe this sort of thing, and many programming tutorials will quite rightly spend a lot of time covering these concepts. In many ways it is not that useful to ROM hacking until you get to analysing what might have happened in the original source to get to here, at this point you probably already know the/a programming language.
An important extra term when discussing this is boundary/alignment. Unless you are writing poetry you probably do not have to make your sentences a given number of letters/words but computers tend to like it more if the data starts on a multiple of a given value (sometimes it might be “byte aligned” but more often it is word aligned or even higher1 ) or involves manipulating a given length of memory (various internal functions of the DS and GBA prefer to only operate on similarly aligned sections of memory).
One link that has some good stuff if you want to go further is the art of assembly but if things are preferred a little closer to conventional maths grinnell.edu have a nice page.
1.1.2 BCD (Binary coded decimal)
Mentioned mainly as it is a nice example on how binary and hex mean very little without context. It is seen in one place on the DS in the firmware and things stemming from it (mainly the clock and calendar functions) as well as older programs, for a while certain processors even had functions in their silicon for it, but it is rarely seen when hacking ROM images these days.
There some minor variations here (the standard 8,4,2 and 1 can make every combination between 0 and 9 but so can 5,3,1 and -1) but they are not commonly seen. As mentioned the standard method is the same as the translation of binary to hexadecimal so bringing back the table with only the relevant entries.
| Decimal | Hexadecimal | Binary |
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
Using the clock example if you wanted to represent the time 15:30 you could figure out a way to encode it or just use BCD
0001 0101 0011 0000 which has a decimal equivalent of 5424 (not 1530) but can quite happily represent the time.
For a quick example of the 5,3,1 and -1 scheme also mentioned
| Decimal | Hexadecimal | Binary |
| 0 | 0 | 0000 |
| 1 | 1 | 0010 |
| 2 | 2 | 0101 |
| 3 | 3 | 0100 |
| 4 | 4 | 1001 or 0110 |
| 5 | 5 | 1000 |
| 6 | 6 | 1010 |
| 7 | 7 | 1101 |
| 8 | 8 | 1100 |
| 9 | 9 | 1110 |
15:30 once more
0010 1000 0100 0000 which has a decimal equivalent of 10304 but according to the scheme above will decode as 1530.
There have been cases of things using it to display fractional values which can be useful as there are certain common things plain hexadecimal struggles with.
1.1.3 Big and little endian
Absolutely vital when dealing with the GBA and DS in any real depth is the concept of endianness. Historical reasons are the main reasons for it existing in the first place although it does have value still, and as many systems use it the aspiring ROM hacker has to know about it. In short where the conventional maths and devices with X86 family chips (most PCs) display the most significant number first devices using ARM chips (and many others) which include the GBA and DS display the least significant bytes first.
In practice it means some locations/lengths might be written as something like A036 0104 when in fact they read 0401 36A0. Although many hex editors will support a change between big and little endian the process by which most of it is rendered readable is usually a flip across so many bits (32 bit flip means 32 bits as above will be flipped, 16 bit flip means only two bytes will be flipped).
Seen as most people code on a PC, or a device that is emulating a PC setup, it is far from unheard of for a device to see a format use the opposite type of endian to what it is.
1.1.4 Signed values, floating point and fixed point
There is also the matter of signed bytes and (floating) point values for as with computers not being able to easily write subscript they tend not to have provisions for negative symbols and values after the “decimal” point either. Do note that some of these methods have since made their way into silicon as well, though the GBA and DS are somewhat lacking here.
Signed values Various methods exist here with popular ones including ones complement, twos complement and excess 7. Each have advantages and some disadvantages depending upon what you are doing although the biggest disadvantages to some of the simpler methods are the inability to do simple maths without conversion and the existence of two values for 0 which makes comparing and acting on the results tricky.
Signed numbers are also one of the reasons for some stats ending at 511 or 127 or similar (it should become apparent why this is very shortly) with the other big reason, assuming the first bit is not simply ignored, is that programmers frequently like using the first bit to encode something or act as a flag of some form (for instance the DS archive format NARC uses it so signify a subdirectory). For another source on the subject grinnell.edu’s CS152 has a nice version.
Sign and magnitude Here the first bit of a value is given over and called a negative flag which is also another name for the method (although the term can be used more generally when dealing with signed numbers), another name is signed magnitude.
Here the first bit is given over to being a sign with the rest of the numbers being interpreted as usual. It is the most similar method to conventional counting/maths. 0 means positive while 1 means negative. 0000 0001 equals 1 and 1000 0001 equals -1
Ones complement For the ones complement a bitwise NOT operation (covered in more detail later but in short it changes every 0 into a 1 and every 1 into a 0) is applied to a positive number making the negative counterpart. It has problems as basic maths can not be done so easily and it has the problem of two values for 0.
0001 becomes 1110
0010 becomes 1101
0011 becomes 1100
Twos complement Marginally more complex than the others mentioned so far is twos complement but as it does not have the pitfalls of the other numbers (two representations of zero and simple maths is possible) it is popular. Here the ones complement is made (bitwise NOT to all the digits) and then 1 is added to the result using conventional binary addition. 0000 becomes 1111 and then 0001 0000 but the other part is ignored.
Examples
Example 1
-1
Postive one is 0001
NOT gives 1110
adding 0001 gives 1111Example 2
-3
Positive three is 0011
A bitwise NOT gives 1100
Adding one 0001 gives 1101Maths example
Similar to the example of 0 above 2 decimal (0010) added to -1 (1111) which gives 0001 0001 and has the leftmost “spillover” ignored.
“Excess 7 Although twos complement and the others will serve you well and form the bulk of everything you come into contact with there is another somewhat more complex method in common use. It can vary a bit depending upon your implementation (the technical/concept name is excess 2^(m-1) where m is the number or binary digits you have to work with) but excess 7 will be used for now.
It becomes more complex and somewhat more important when fractional numbers arise (covered in the section below). In practice it is a kind of combination of the basic signed magnitude idea and twos compliment. As mentioned this is sticking with excess 7 for the example but scaling up is fairly logical.
In this system the the first bit is used to indicate the sign (although not necessarily the sign of the final number) leaving the remaining 7 (excess 7) to do what needs to be done. So far not very different to anything covered but this is where the trick happens although an example before it is covered in earnest.
In years past you might have been encouraged to just make numbers huge as a workaround for having to deal with negative numbers.
The equation
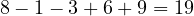
8 - 1- 3+ 6 +9 = 19
A simple equation but with a calculator or in your head it is quite possible to make a mistake and mess the whole thing up.
Adding in this case ten to all the numbers makes them all positive
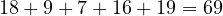
18+ 9 +7 + 16+ 19 = 69
Five numbers all 10 larger makes the result “out” by 50 but plain addition is far easier to avoid making a mistake in.
The reason for the digression to simple maths tricks is a similar principle gets used for excess 7.
In the case of the excess 7 (also called 8 bit excess 127) this is usually 01111111 or 127 in decimal. Here the value you want to encode is either taken (positive numbers) or added to (negative numbers) from this value. In theory, and so probably somewhere in a game out there, the excess does not have to be 127.
If you prefer it could be seen as counting starting at the lowest possible number which would be “-(-1 +2^m)” or for 8 bits “-(-1 + 2^7)” which is negative 127 and call that the starting / “zero” value. 0 (as in nought) is then the bias value. It has the advantage of being easily compared with other numbers so it is worth knowing about.
Examples
# Number to encode -7 or (-) 0000 0111
0111 1111 – 0000 0111 = 0111 1000
# Number to encode 18 or 0001 0010
0111 1111 + 0001 0010 = 1001 0001Examples
0000 0000 -127
0000 0001 -126
0000 0010 -125
0111 1111 0
1000 0000 +1
1000 0001 1111 1111 +128In practice/the real world this is covered by the near universal standard IEEE 754 which is more commonly seen when dealing with floating point numbers. You could make another method but nobody really does and hardware is built to use it so again nobody does, give or take a few things using fixed point numbers. Here 32bits or more can be used with the first being the sign, the next being the bias value and the rest being the encoded number in question. Speaking of fractional numbers though
Fractional numbers and real numbers Fractional numbers are usually done using a so called “floating point”, however the GBA and DS do make extensive use of fixed point numbers for various parts of the hardware including 2d transformations and 3d and will be covered shortly. The idea of leaving things as values and only calculating them at the last moment is encouraged in programming but in hardware or the final representation this can be tricky and as that is where ROM hackers spend most of their time it will be noted and nothing much else said on the subject.
Floating point On the face of it floating point appears related to the excess 7 method of displaying signed numbers, in practice it is actually closer to the standard scientific notation for displaying large numbers. The concept of this then is the idea of floating point numbers, in essence they are
- A sign value
- A multiplier (actually an exponent) to make sure the “decimal” point gets where it needs to be
- The number itself but without the 1 part as that is assumed to be 1 so as to be able to save a bit.
For 3. above much like you would never write 0.31x10^-3, unless you are an engineer where the used powers are usually a multiple of three, it is always assumed the first bit is 1, as you are working in binary that means the only value it can be is 1 and you can leave it out of the number that is transmitted as long as you remember to reconstruct it.
It probably does not take a great leap of imagination to see how this gets very complex to operate with multiple values (different “powers” or not) very fast. To this end even though most software development kits and systems will feature abilities to handle such things their use is ideally saved for when there is no other option, indeed newer/high performance systems often have their computer power compared by how many flops (floating point operations per second) or indeed criticised on their lack of support for various versions of floating point (single precision, double precision…..). Unlike binary and hexadecimal above the ability to decode it is something you should be able to run through but most will expect you to use tools to handle it.
There is a class of compression based on this idea known as arithmetic coding. It works on the idea that for the file might represent it is still a number and some numbers can can be represented shorter by encoding them as a floating point.
The short version
32 bits long the first bit is the sign of the multiplier, the next 8 bits are the value of the exponent of the multiplier in excess 7 notation and the final bits are the basic value that needs multiplying save for the “hidden” 1 value which the fractional part gets added to.
That is a bit wordy so examples
Decoding 40a4cccd hex
The binary representation is as follows
0100 0000 1010 0100 1100 1100 1100 1101
0 starting means it is positive.
The excess 7 bits
1000 0001
0111 1111 + ???? ???? = 1000 0001
???? ???? = 0000 0010 = 2 decimal (leading to 2^2 or 4)
Taking the remaining section and adding the invisible 1
1010 0100 1100 1100 1100 1101
Much like binary is powers of two the fractional part goes the other way and decreases in powers of two so taking that pattern and checking off the pattern against it.
1 0 0.25 0 0 0.03125 and so on
Using just the numbers there 1.28125
Multiplying by 4 gives 5.125
Short of the actual number it is supposed to represent which is 5.15 but if you continued adding numbers from the binary pattern it would get very near there.
Representing 3.14
Positive so first is 0
Dividing by 2 renders it as 1. something and 2^1 = 2
2 in excess 7 is 10000000
0.57 is the number that needs representing.
0.5 + 0 + 0 + 0.0625 and so on
For now stopping there
10010000000000000000000
Working back through leaves it at
01000000010010000000000000000000 binary or 4048 0000 hex
Decoding that though gives 3.125 so the pattern should have been continued further
In practice it ends up as
10010001111010111000011
Which combined with the rest gives
4048f5c3 hex.
The slightly longer version
Single precision (32 bits) and double precision (64 bits) are the most common versions of floating point with anything beyond that (save perhaps quad precision in some hardware) usually being relegated to (very slow) software methods.
Also the exponent values in theory at least range from -126 to 127 (00000001 and 11111110) meaning the all 0 and the all 1 values are not available. In practice these are used as follows
0
All 0 indicates exact 0 or more accurately values smaller than the lowest feasible value.
1
All 1 indicates either positive or negative infinity for the all 1 values assuming the mantissa section has nothing in it. If the mantissa does have something in it then it means an error like divide by 0 or something similar (NaN aka not a number).
For more IEEE floating-point representations of real numbershas a basic overview and What Every Computer Scientist Should Know About Floating-Point Arithmetic has a far more in depth discussion and historical analysis. If you just want something to toy with to get it sorted in your head FloatConverter is quite good.
To make up for some of the shortcomings of the method there are two common functions that are used when dealing with such things.
Ceiling In short round up to a given value (or multiple thereof) regardless of what a conventional round would do. Not necessarily limited to fractional numbers either.
Floor In short round down to a given value regardless of what a conventional round would do. Also not necessarily limited to fractional numbers.
Fixed point values Floating point is used everywhere in computing (especially in 3d and mapping of things in 3d, something you may have seen the occasional game do) and it is quite costly in terms of resources so fixed point appears.
Fixed point attempts to work around some of the issues with floating point at the potential cost of some accuracy and some flexibility. It is seen in parts of the DS 3d system among other things where 4 bits “natural number” 12 bits “fractional” is often of the order of the day. That is to say the computer assumes all numbers after a given binary digit are fractional. Some instead prefer to view it as a range type function with 0000 to 1111 representing the difference between two whole numbers (or in the case of sine and cosine -1 to 1).
Timers are quite commonly made like this although they can also just be a multiple, the “timer” used for the DS SSEQ audio format being a good example of the latter.
What the numbers mean is usually either the logical extension of the binary “powers” (2^-1=0.5 decimal, 2^-2 = 0.25 decimal…..) or they count again and the number after the point is effectively assumed to be a normal number. Binary coded decimal, almost invariably in the 8421 arrangement, can also appear here.
As with signed values their use prevents the number from being read as a simple integer and used in simple maths although with a bit of shifting, rotating and such you can get quite a bit done and even do some basic comparing and maths. Speaking of shifting and rotating
There are hardware limits on the GBA and DS depending upon what you are doing (it will be covered in graphics and compression later) but in theory nothing needs to be word aligned. Most things will be word or aligned to an even larger multiple though so unless you can demonstrate otherwise stick with what you first see. Certainly for the initial passes of most files assume at least byte alignment.↩︎