1.2 Hex operations
Hexadecimal is just numbering but there are common things done to it that file formats use, the internal logic of the computer will use and can be used to quickly and easily manipulate something that needs manipulating.
1.2.1 Shift
Right hand and left hand shift are useful when you need to chop off a bit from a value, you need to generate a value where you can not fit it into a smaller length than the destination or in some formats which leave things in an unshifted form for whatever reason. In practice 32 bits allows for a lot of address and 31 bits can still quite easily handle most GBA and DS addressing needs so the upper bit can be used to indicate things, as indeed NARC files do so as to indicate a subdirectory. Moreover lots of the DS internals only need a few bits for things they do so they are combined with other sometimes unrelated things which you might need to lose to see what is going on. In a hex editor you would probably be better advised to use Boolean logic (covered in a moment) rather than shifts but in hardware it can go either way.
A shift can be right hand (you shift the numbers to the right losing the leftmost piece of data) or you shift to the left losing the rightmost piece of data.
It is also useful as a quick multiplier; think how you technically shift the numbers when you multiply or divide by 10 in decimal, albeit here you multiply or divide by 2 instead.
There is also the distinction of logical shift and arithmetic shift where in the case of the latter you do not lose the data if you shift left and then shift right. You can also do block shifts but they are just a special case which usually means a given number of bits are shifted.
1.2.2 Rotate
Related to shift but where you lose data if you shift it appears in the other side when you rotate.
1011 rotates left by 1 bit makes 0111
1.2.3 Flip
Flip is most useful when you are working around big and little endian. It was already seen when big and little endian were covered above but a 32 bit flip of A036 0104 reads 0401 36A0.
In some cases it can be useful to flip larger or smaller values, for instance although many formats will use a full 32 bits for a length the file might be very short and only need the first 16 bits. More useful (and not often a function of hex editors) the GBA 4BPP image format uses 4 bits per pixel but will flip them between storage and being on the screen.
In the figure below you can see the hex that represents the highlighted tile (it is the icon from the wifi version of Yakuman DS, a competitive Mahjong title).
- In the first line you can see 0000 D0DD where the pink pixels (in practice they would be transparent but more on that when graphics are discussed) which are represented by 0 in this case run for 5 pixels.
- In the next line you can see 4 pink pixels as they are but then the grey pixel (in this case D) is after the F value which represents the white pixel
- In the next line you can see the cream coloured pixel (E) be second to last as opposed to actually last. It it done because that is how the hardware works/expects things but it can make it tricky if you are trying to simply edit it.
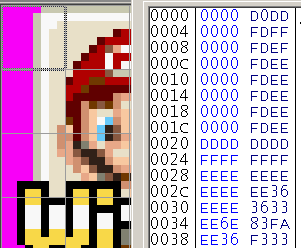
PIC
1.2.4 Boolean logic
Often a more useful set of techniques than basic shifts and the other operations covered already. There are several types although you will probably see patterns soon enough (mainly that the NAND, NOR and XNOR are just the inverse of their counterparts). Boolean logic exists in two big areas ROM hacking and related pursuits might be concerned with; one is programming and the other is electronic logic where they perform identical functions but in some ways are thought of a bit differently.
Here is probably useful to discuss the idea of high and low as it applies to computing and electronics. In the vast majority of cases (especially software and ROM hacking) you should always assume that unless otherwise stated a high value corresponds to 1 and a low value corresponds to 0. This is unlike some other things in this section where you will usually want to seek clarification for things (what method of negative or point numbers you are using for instance). There is however a variation on this called negative edge logic (referring to certain chips that change on the falling edge of a clock pulse) that can be described with the opposite where 0 is high and 1 is low.
Examples will be done in binary.
NOT aka inverse Does what it says and flips every bit.
1001 1110 becomes 0110 0001
AND Here you take two numbers (preferably of equal length but if not the shorter sequence is repeated as appropriate in most cases) and combine the outcome so that only if both inputs are high the result is high
1100 1111 AND 1010 0100 becomes 1000 0100
NAND Much like AND you take two numbers and put them together but rather than if both are high this is if both are low. It is most useful as it is a fundamental logic operation; you can stack NAND operations or indeed NAND gates in such a way that you can make any other Boolean operation.
1100 1111 NAND 1010 0100 becomes 0111 1011
OR Again two numbers but if any one of the inputs it high the result is high.
1100 1111 OR 1010 0100 becomes 1110 1111
NOR Two numbers but only high if both inputs are low
1100 1111 NOR 1010 0100 becomes 0001 0000
XOR Two numbers but only high if only one input is high. Useful as encryption by itself and the basis of many more useful encryption methods. As a quick aside there are serious downsides when it comes to actually being used as encryption, if done properly it is one of the few that can not be broken with enough computing power. Also where the others can easily have multiple inputs in electronics a multiple input XOR is tricky at best.
1100 1111 XOR 1010 0100 becomes 0110 1011
XNOR Two inputs, only high outputs when none or both inputs are the same. Being the inverse of XOR it has similar problems to it.
1100 1111 XNOR 1010 0100 becomes 1001 0100
Discussion of Boolean logic. The most useful in day to day ROM hacking are probably NOT, AND, OR and, purely because of the encryption, XOR.
NOT aka inverse is useful on many occasions for many things especially in graphics (it might not be quite that simple in practice but inverting colours is quite common). Also useful to corrupt data and recover it easily (you just invert it back).
AND is useful to remove certain bits, for instance if you want to remove the highest bit in a byte just AND the result with 0111 1111 and whatever the rest is will stay the same but the highest bit will be 0 regardless.
OR is useful if you want to set a certain bit high, for instance to set the highest bit in a byte high just OR the result with 1000 0000 and the first bit will be set high regardless but the rest will only be high if they were to begin with.
XOR is also used a few times in the internals of the GBA and DS and is used extensively as simple protection at points in cheat devices and things like the GBA e reader.
An aside on logical/relational operators They share the same name and broad function as the boolean logic but here they are used as checks to see if both inputs meet a given condition. In C type languages it runs as follows
AND checks to see if both inputs are non 0 and returns true if it is the case
OR checks to see if just one input is non 0 and returns true if it is the case
NOT merely reverses the output of the other functions.
As far as most of ROM hacking is concerned this will usually be interpreted closer to assembly where compares and branching will be used instead.
Equally a right hand logical shift is different from a conventional right hand shift in that it will retain the most significant bit
1000 1110 right shifted by 1 makes for 1100 0111
1.2.5 Hex Mathematics.
Some people can operate in hexadecimal but most of the time the maths resembles long division and long form maths. It is quite useful to know as… quickfire round what is 9 + 3 in hex.
The answer is C but courtesy of probably using decimal all your life your immediate thought might well have been 12 which could well mess your entire hack up if you put that into the ROM.
Subtraction works much the same way until you get to negative (signed) numbers in which case you get to figure out what method you are using for it.
Multiplication is easy enough
1D x 09 is 10 x 9 + 0D x 9 or 90 + 75 = 105
Division is a pain and more importantly depends on the programming language function used; many basic methods will chop off the stuff after the “decimal” point where others will turn it into a floating number. Floating point might not be that accurate as hex is somewhat less capable of displaying the results of common divisions, not to mention it will be rounded at some point. Such a trick is often used to confuse, and so teach, new programmers and even catches out older ones; finance packages are especially troubled by this for if they miss a couple of rounding points it can result in big amounts of money not going where it needs to go. There are however a few concepts worth noting as they crop up in programming languages and the processors they run on
Mod As mentioned some basic hexadecimal divide functions will leave you with just the whole number part of the result (99 divided by 6 is 16.5 but many divide functions would just give you 16). Mod is then a function that gives you the remainder as a whole number (99 divided by 6 is 16 remainder 3) which you can leave in the hope it will be multiplied back later or feed to another command (many divide functions struggle with large numbers and prefer small ones).
Abs(olute) Potentially confusingly regular maths sometimes also calls this modulus with the shorthand sometimes being “mod”. Depending upon how far you want to take maths it can get quite complex but the short version is abs value of a number is just the number (always positive) without the sign. It is then quite useful to feed into functions so you can simplify them or the resulting maths.